Что такое Египетский треугольник на стройке? В чем его особенность

Индивидуальное значение

Тату «треугольник» для каждого человека является чем-то особенным

Так, например, для девушек эта простая на вид фигура, может означать кое-что важное и глубокомысленное. Треугольник – отображение трех циклов жизни практически любой женщины. Это девичество, материнство и старость

Не все могут додуматься до такого. Однако подобное разъяснение существует уже давно, и многие набивают треугольник намеренно с этой целью

Это девичество, материнство и старость. Не все могут додуматься до такого. Однако подобное разъяснение существует уже давно, и многие набивают треугольник намеренно с этой целью.

Для мужчин же фигура означает кое-что другое. Треугольник также символизирует «троицу», однако в данном случае это не цикл жизни, а качества. Если быть точнее, то мудрость, сила и красота

К слову, очень важно, какой был выбран участок для татуировки. Он способен усилить, подчеркнуть придаваемый смысл. Чаще всего такие тату можно видеть на запястье, предплечье или на затылке

Это самые популярные варианты исполнения. Но на самом деле человек сам выбирает место

Чаще всего такие тату можно видеть на запястье, предплечье или на затылке. Это самые популярные варианты исполнения. Но на самом деле человек сам выбирает место.

Иногда треугольники закрашивают. Цвет также означает очень многое. Красный символизирует страсть, черный – негатив, зеленый – безопасность, оранжевый – жизнелюбие. Оттенок действительно может рассказать о многом, так что выбирать его нужно особенно тщательно. И, кстати, стоит учитывать, что на коже выбранный цвет всегда смотрится на 2-3 тона темнее. Следует об этом знать и подбирать краску с осознанием данного факта.

Как добывали камень?

Современные достижения науки и техники позволяют археологам точно определить карьеры и технологии добычи камня в Древнем Египте. Сегодня точно известно, что при возведении усыпальниц использовались известняк, гранит, кварцит, базальт.

• Известняк добывали каменными молотами и бронзовыми кирками, долотами.
• Твердые породы отбивали долеритовыми инструментами, затем распиливали их. В качестве абразивного материала для беззубых пил того времени использовался кварцевый песок.
• Гранитные блоки выламывали, используя разбухающие от жидкости деревянные клинья.

Блоки из известняка использовались в качестве основного материала – их заметно у входа. Весил каждый блок около 2 тонн. С внешней стороны блоки правильной формы, прилегание плотное. Высота камней разная. 

Во внутренних коридорах пирамиды Хеопса видны декоративные гранитные блоки. Они тонкие, идеально подогнаны друг к другу, чтобы не было зазоров.

В погребальных камерах установлены монолитные гранитные плиты. В камере фараона Хеопса их 52, их вес доходит до 20-40 тонн. Такие мегалиты добывали и доставляли на строительство из дальних карьеров. Остается вопрос, как такой вес строители поднимали на высоту?

История

Знаменитый греческий математик и философ Пифагор Самосский, давший свое имя теореме, жил 2,5 тыс. лет назад. Биография этого выдающегося ученого мало изучена, однако до сегодняшнего времени все же дошли некоторые .

По просьбе Фалеса, с целью изучения математики и астрономии, в 535 году до нашей эры он отправился в длинное путешествие в Египет и Вавилон. В Египте среди бескрайнего простора пустыни он увидел пирамиды, изумляющие своими огромными размерами и стройными геометрическими формами. Стоит отметить, что Пифагор их лицезрел в несколько ином виде, чем тот, в котором видят туристы сейчас. Это были невообразимо огромные для того времени сооружения с четкими ровными гранями на фоне прилегающих храмов поменьше, для жен, детей и других родственников . Кроме прямого назначения (усыпальницы и хранителя священного тела фараона) пирамиды сооружались и как символы величия, богатства и могущества Египта.

И вот Пифагор в ходе тщательного изучения этих конструкций заметил строгую закономерность в соотношении размеров и форм сооружений. Размерам Египетского треугольника соответствует пирамида Хеопса, она считалась священной и носила особенный магический смысл.

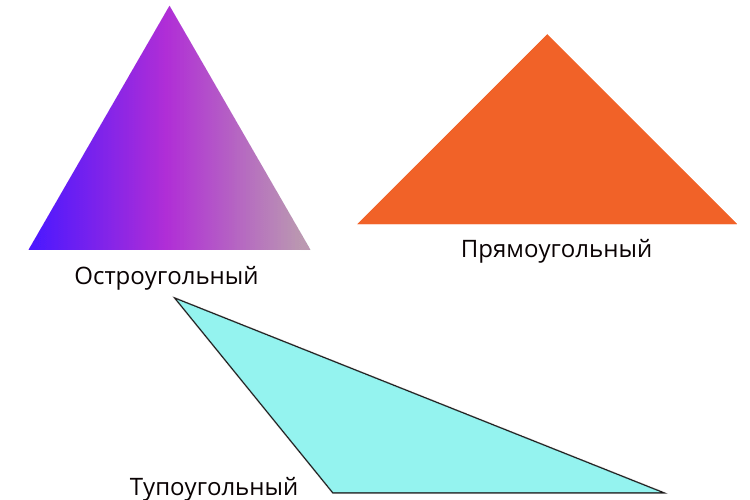
Виды треугольников по углам

Определение. Остроугольным треугольником называется треугольник, у которого все углы острые.

Определение. Прямоугольным треугольником называется треугольник с прямым углом.

Определение. Тупоугольным треугольником называется треугольник с тупым углом.

— Так, про треугольник понятно, — задумчиво сказал Бим. — Хотя — нет, не совсем понятно. Вот у этих конфет по 3 угла, но они разные.

— Конечно, — ответила Оля. — У всех этих конфет разные углы. Вот конфета, у которой все углы острые. Мы знаем, что острый угол меньше, чем прямой.

Оля достала листочек в клеточку и приложила к нему конфету.

 — Поглядите сюда. У клеточки одна сторона идет по горизонтали, а другая по вертикали. Если одну сторону конфеты приложить к горизонтали, то вторая сторона конфеты пойдет ниже вертикали клеточки, значит угол между сторонами треугольника острый. Проверим еще два угла, они оба острые. Все три угла — острые. Треугольник с тремя острыми углами называется остроугольным.

— Дай, пожалуйста, листочек в клеточку, — попросил Бим.

— С удовольствием, — ответила Оля.

Бим приложил другую конфету к листочку.

— Что-то у меня не получается. У конфеты два угла острых, а стороны третьего угла совпадают с вертикальной и горизонтальной сторонами клеточки…

— Так это уже другой вид треугольника — прямоугольный треугольник! — крикнул Коля. — Треугольник, у которого один угол прямой, называют прямоугольным.

Бом тоже попросил листочек в клеточку и приложил еще одну конфету.

— У меня совсем по-другому. В этой конфете сторона одного угла вообще в клеточку не попала, где-то вне клеточки. Что же это за угол такой?

— Такой угол называется тупым, он больше, чем прямой угол, — заметил Вася. — И треугольник, у которого есть тупой угол, называется тупоугольным треугольником.

Процесс сборки каменных блоков

Современники разгадали технологию строительства пирамид в Древнем Египте, точнее, механизм подъема многотонных гранитных блоков на высоту. Секрет в том, что 20-30-тонные глыбы строители не поднимали, а готовили его по месту.

Для этого сооружали опалубку из древесины египетского кедра и готовили бетонный раствор с добавлением гранитной крошки. Часто в раствор добавляли мраморную крошку, оставшуюся при дроблении камней в карьерах.

Раствор готовили на высоте, а воду для него и другие материалы строители поднимали по пандусу. Когда бетон застывал наверху, получался прочный камень.

Научным подтверждением описанной технологии строительства стали результаты исследования, опубликованные в авторитетном научном издании «Journal of the American Ceramic Society» в ноябре 2006 года.

В статье говорилось о том, как группа ученых исследовала каменные блоки пирамид Древнего Египта посредством спектроскопии и светомикроскопии. В ходе анализа выяснилось, что в состав образцов входят компоненты, включающие кремний, кальций и магний в пропорциях, не характерных для натурального известняка и другого камня природного происхождения.

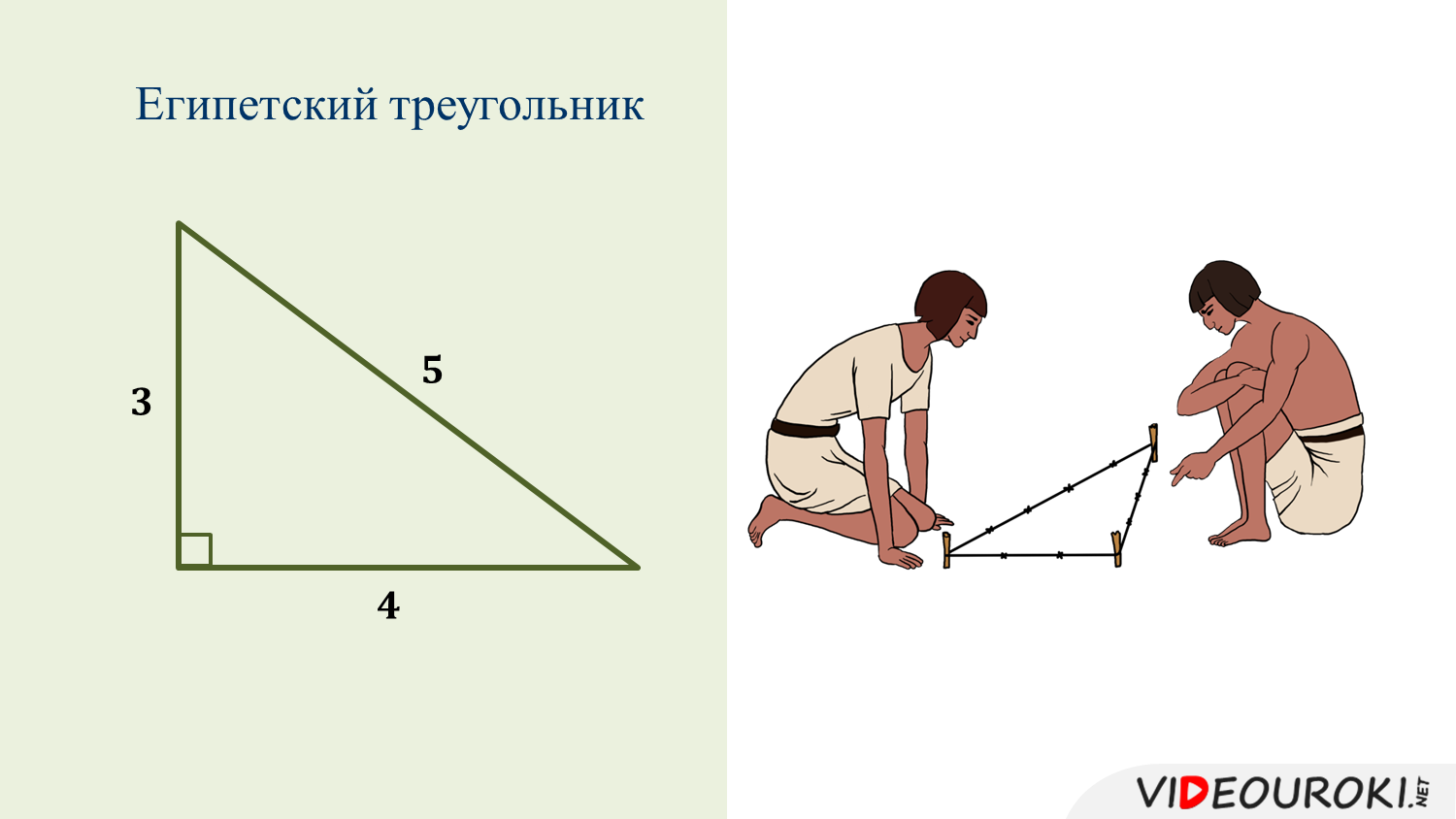
Доказательство

При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным. Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.

Египетский треугольник в строительстве

Мы действительно не знаем с уверенностью, как пирамида была разработана, поскольку это знание могло существовать, а затем было потеряно. У строителей такой невероятной архитектуры, возможно, были гораздо большие знания и утонченность, чем мы можем знать, и возможно, что пи, фи или оба, как мы понимаем их сегодня, могли быть факторами в конструкции пирамиды. Возможно, они выбрали другие подходы, которые привели к почти одинаковой геометрии.

Остается один факт и один интересный вопрос

Ниже представлена ​​геометрия и расчеты. Другая нумерологическая тайна в некоторых пирамидах – знаменитая аксиома Пифагора. Некоторые авторы утверждают, что это еще один признак ранних технических культур, другие считают это доказательством того, что пирамиды намного моложе мысли. Давайте посмотрим на эту тайну. Аксиома Пифагора имеет особый вид треугольников, квадратноугольных. Эти треугольники имеют две стороны, образующие квадратный угол друг с другом, и третью сторону, соединяющую их, гипотенузу.

>>Геометрия: Египетский треугольник. Полные уроки

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Qpstol.ru – “Купистол” стремится предоставить лучший сервис своим клиентам. 5 звёзд на ЯндексМаркет.
Lifemebel.ru – гипермаркет мебели с оборотом более 50 000 000 в месяц!
Ezakaz.ru – Представленная на сайте мебель изготавливается на собственной фабрике в Москве, а так же проверенными производителями из Китая, Индонезии, Малайзии и Тайваня.”

В области геометрии египтяне знали точные формулы для площади прямоугольника, треугольника, трапеции и сферы, могли высчитывать объемы параллелепипеда, цилиндра и пирамид.

Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как; эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику.

Египтяне предполагали, что (погрешность менее 1 %).

Формула площади круга с диаметром d имела вид:

Ещё одна ошибка содержится в Акмимском папирусе: автор считает, что если радиус круга A есть среднее арифметическое радиусов двух других кругов B и C, то и площадь круга A есть среднее арифметическое площадей кругов B и C.

Вычисление объема усеченной пирамиды: пусть мы имеем правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по оригинальной, но точной формуле:

См. также

Шаблон:Викисловарь
Шаблон:Кол

• Барицентр
• Барицентрические координаты
• Высота треугольника
• Вписанная окружность
• Вписанная и вневписанные в треугольник окружности
• Замечательные точки треугольника
• Инцентр
• Окружность
• Окружность девяти точек
• Ортоцентр
• Правильный треугольник
• Признаки подобия треугольников
• Прямая Симсона
• Прямая Эйлера
• Прямоугольный треугольник
• Равносторонний треугольник
• Равнобедренный треугольник
• Средняя линия треугольника
• Сферический треугольник
• Теорема косинусов
• Теорема о сумме углов треугольника
• Теорема о трезубце
• Теорема синусов
• Теорема Харкорта
• Точки Аполлония
• Точка Жергона
• Точка Лемуана
• Точка Нагеля
• Точки Наполеона
• Точка Парри
• Точка Понселе
• Точки Торричелли
• Точка Ферма
• Треугольник Рёло
• Трилинейные координаты
• Формула Герона
• Центр девяти точек
• Центр тяжести
• Центр Шпикера
• Центроид
• Центроид треугольника

Эллипс Штейнера

Шаблон:Конец кол

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Стороны конструкции имеют следующее соотношение друг к другу:

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять

В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

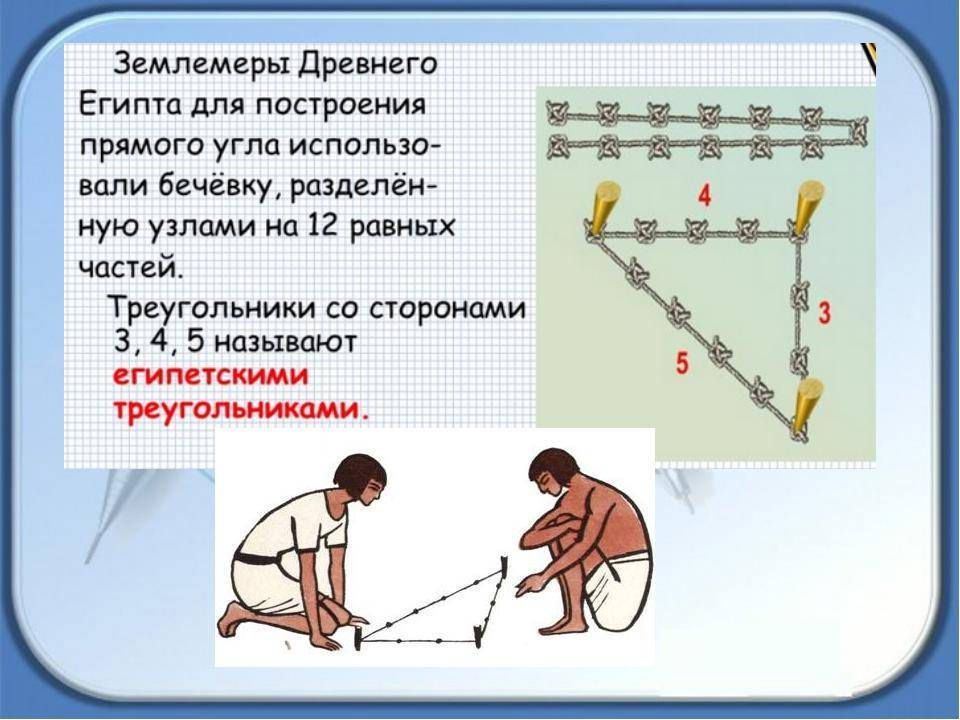
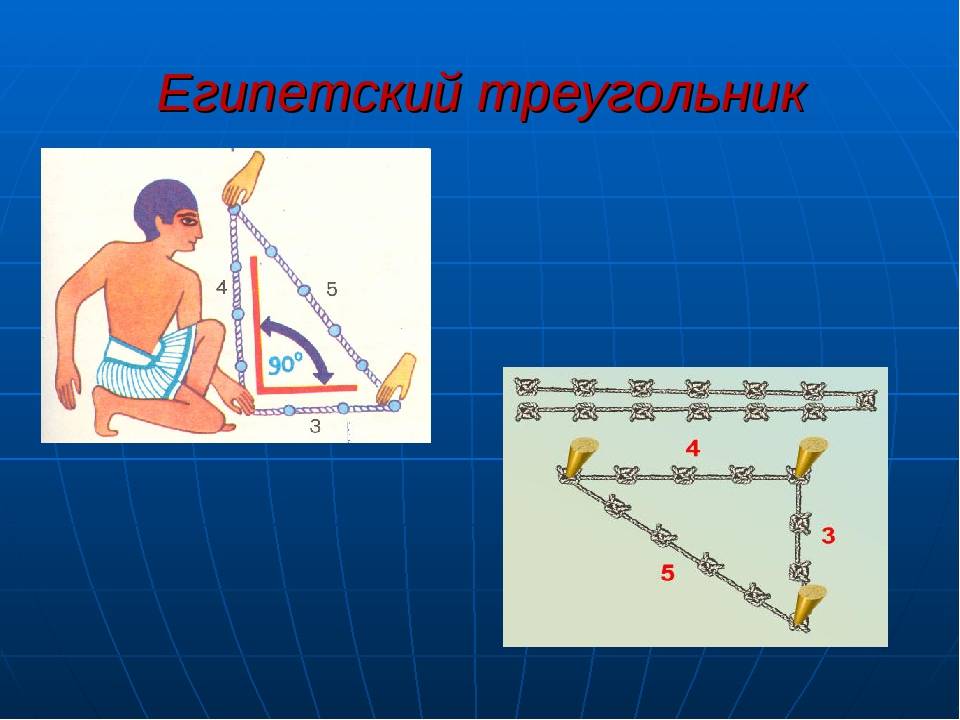
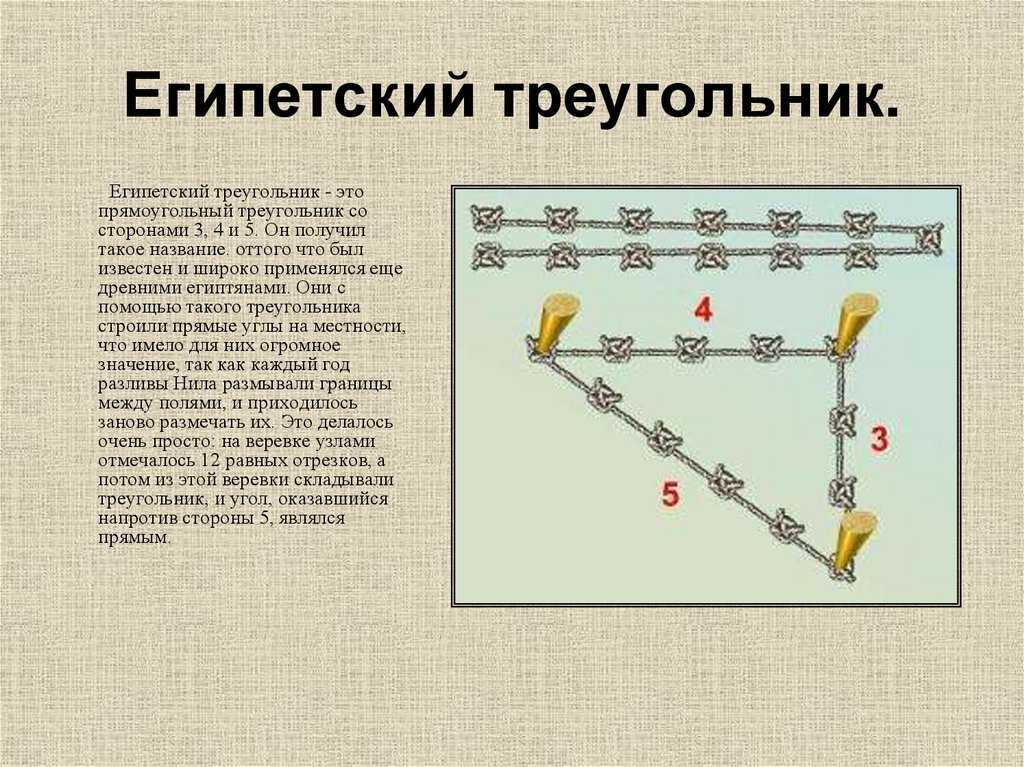
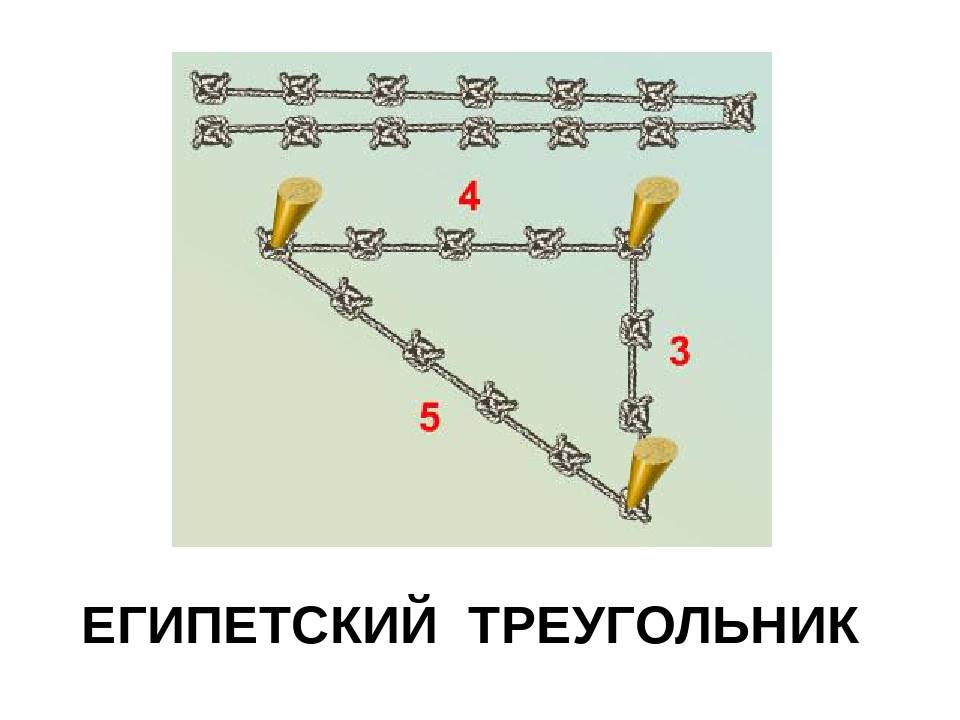
Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть

Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках

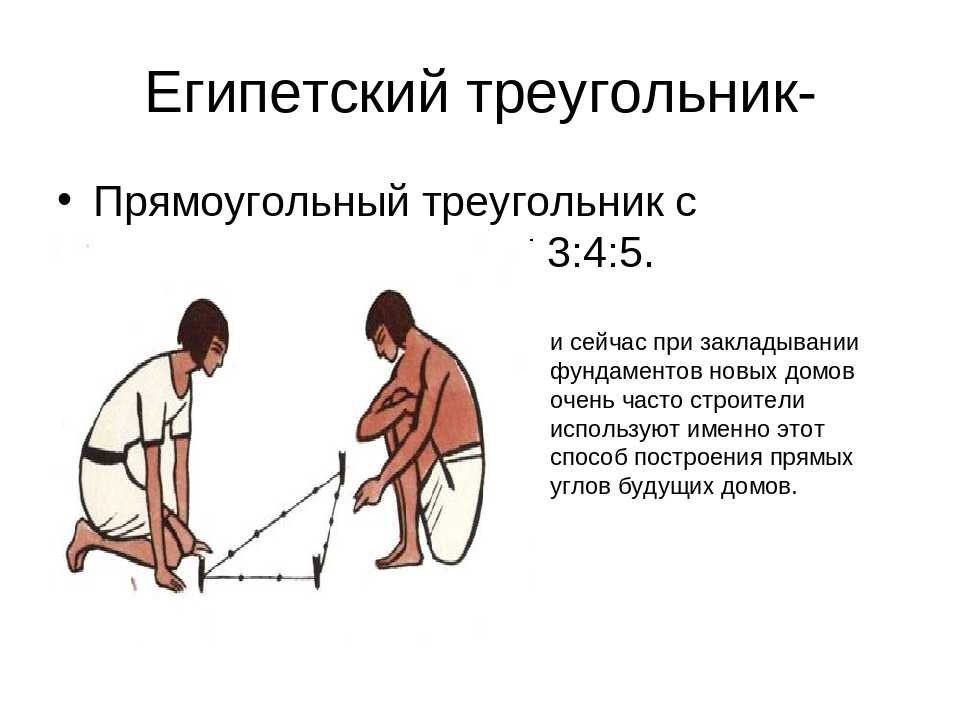
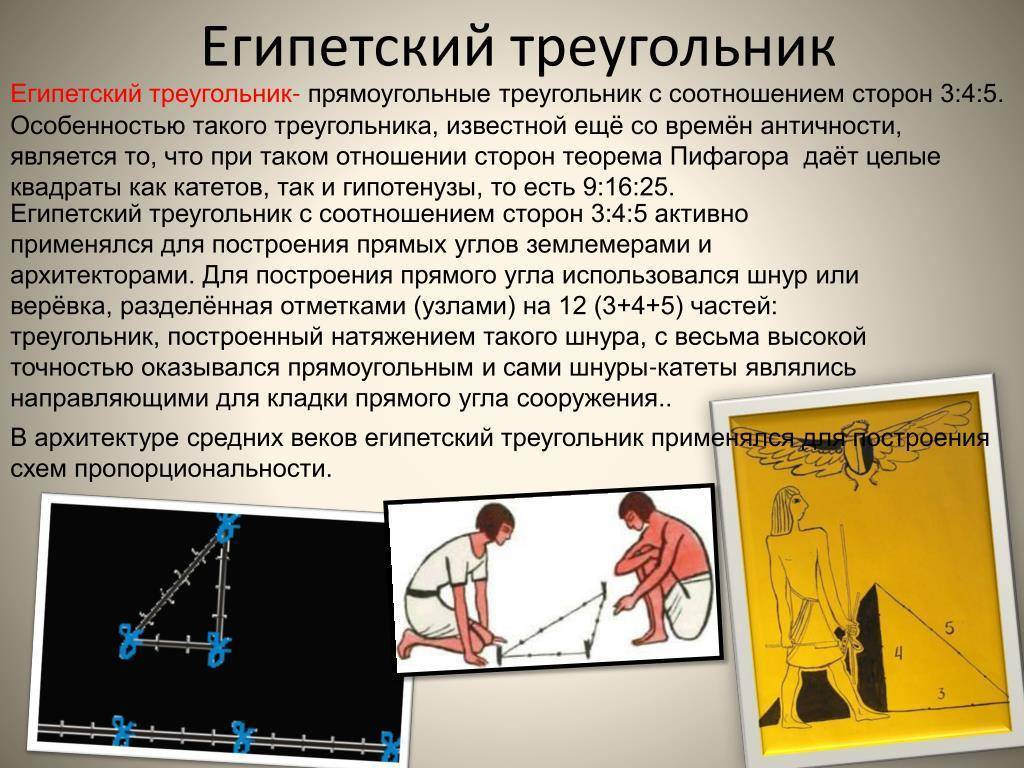
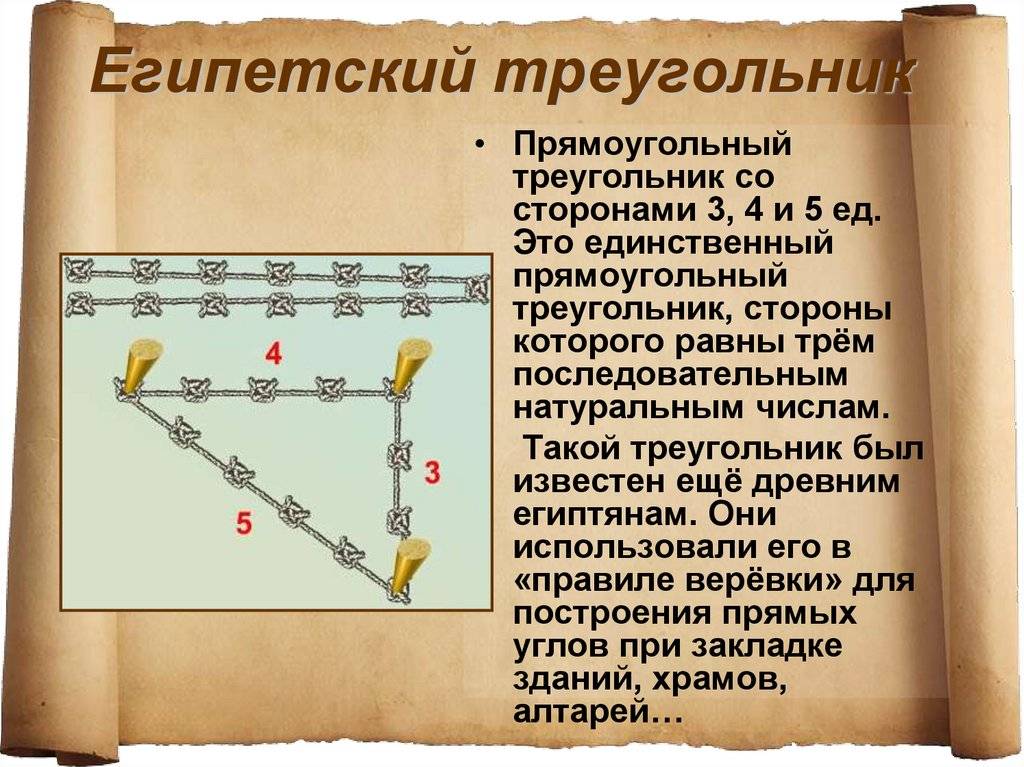
Применение

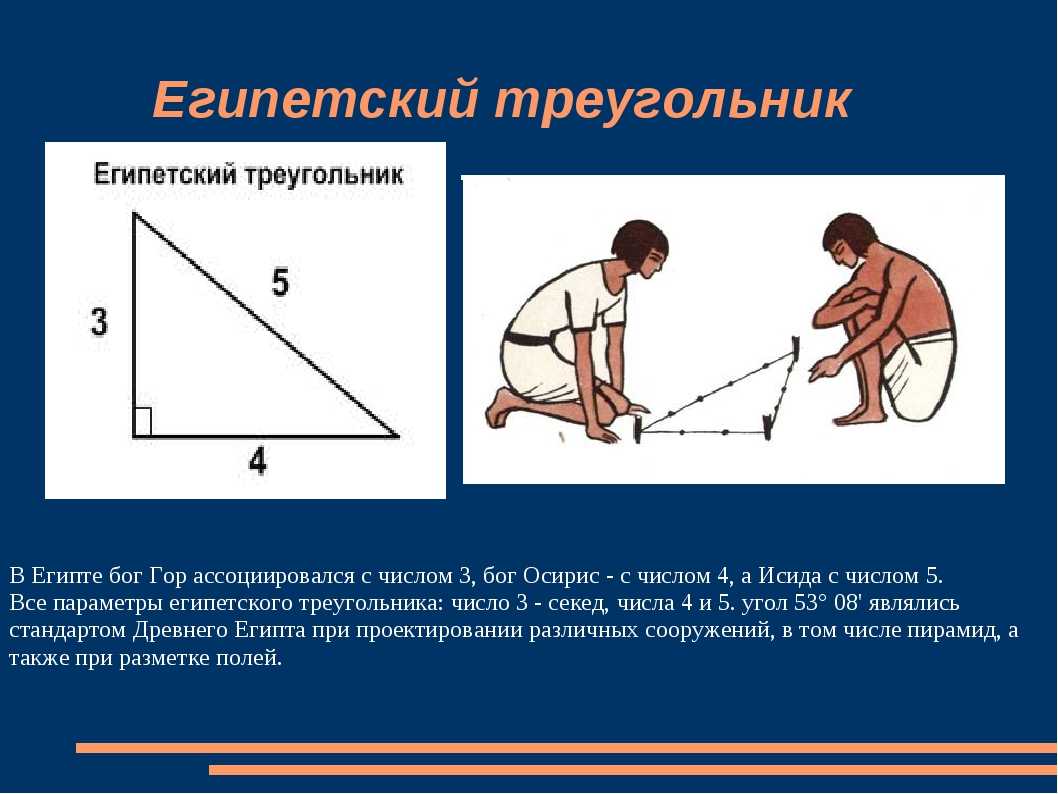
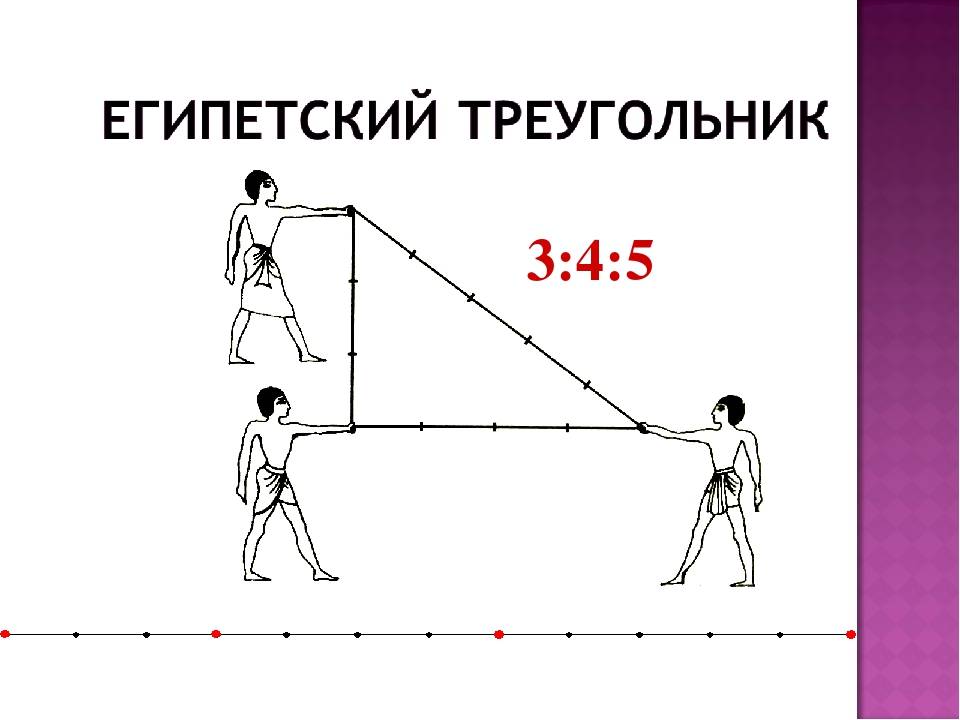
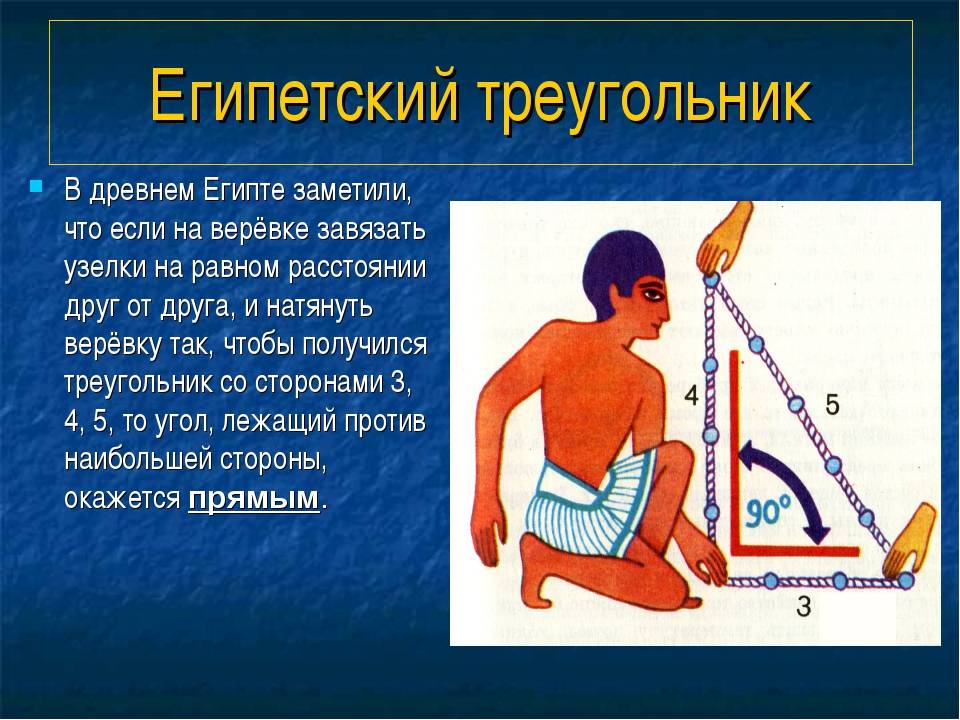
Ка-ж-дый, кто внимательно слушал в школе преподавателя геометрии, очень хорошо знаком с тем, что представляет собой египетский треугольник. От других видов подобных с углом в 90 градусов он отличается особым соотношением сторон. Когда человек впервые слышит словосочетание «египетский треугольник», на ум приходят картины величественных пирамид и фараонов. А что же говорит история?

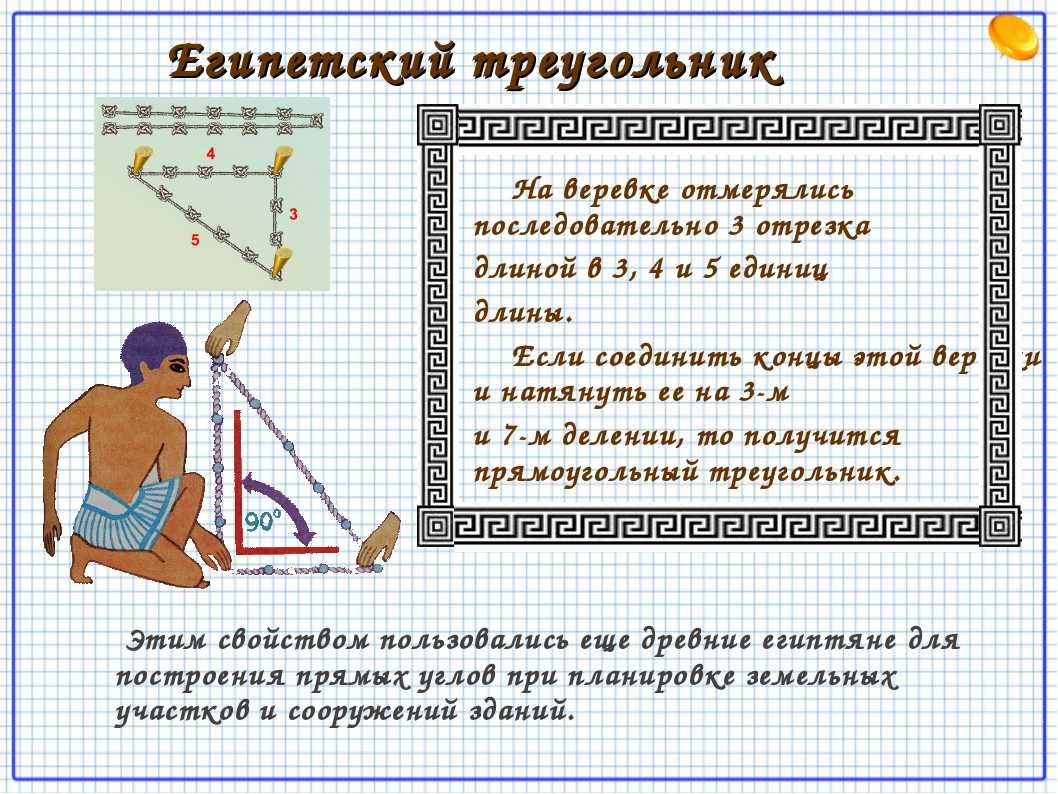
Как это всегда бывает, в отношении названия «египетский треугольник» есть несколько теорий. Согласно одной из них, известная теорема Пифагора увидела свет именно благодаря данной фигуре. В 535 году до н.э. Пифагор, следуя рекомендации Фалеса, отправился в Египет с целью восполнить некоторые пробелы в познаниях математики и астрономии

Там он обратил внимание на особенности работы египетских землемеров. Они очень необычным способом выполняли построение с прямым углом, стороны которой были взаимосвязаны одна с другой соотношением 3-4-5

Данный математический ряд позволял относительно легко связать квадраты всех трех сторон одним правилом. Именно так и возникла знаменитая теорема. А египетский треугольник как раз и есть та самая фигура, натолкнувшая Пифагора на гениальнейшее решение. Согласно другим историческим данным, фигуре дали название греки: в то время они часто гостили в Египте, где могли заинтересоваться работой землемеров. Существует вероятность, что, как это часто бывает с научными открытиями, обе истории произошли одновременно, поэтому нельзя с уверенностью утверждать, кто же придумал первым название «египетский треугольник». Свойства его удивительны и, разумеется, не исчерпываются одним лишь соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применение к нему теоремы Пифагора позволяет получить целые числа квадратов гипотенузы и катетов: 9-16-25. Конечно, это может быть простым совпадением. Но как в таком случае объяснить тот факт, что египтяне считали «свой» треугольник священным? Они верили в его взаимосвязь со всей Вселенной.

После того, как информация об этой необычной геометрической фигуре стала общедоступной, в мире начались поиски других подобных треугольников с целочисленными сторонами. Было очевидно, что они существуют

Но важность вопроса состояла не в том, чтобы просто выполнить математические расчеты, а проверить «священные» свойства. Египтяне, при всей своей необычности, никогда не считались глупыми – ученые до сих пор не могут объяснить, как именно были возведены пирамиды

А здесь, вдруг, обычной фигуре приписывалась связь с Природой и Вселенной. И, действительно, найденная клинопись содержит указания о подобном треугольнике со стороной, размер которой описывается 15-значным числом. В настоящее время египетский треугольник, углы которого равны 90 (прямой), 53 и 37 градусов, находят в совершенно неожиданных местах. К примеру, при изучении поведения молекул самой обыкновенной воды, выяснилось, что смена сопровождается перестройкой пространственной конфигурации молекул, в которой можно увидеть…тот самый египетский треугольник. Если вспомнить, что состоит из трех атомов, то можно говорить об условных трех сторонах. Конечно, о полном совпадении знаменитого соотношения речь не идет, но получаемые числа очень и очень близки к искомым. Не потому ли египтяне признавали за своим «3-4-5» треугольником символический ключ к природным явлениям и тайнам Вселенной? Ведь вода, как известно, основа жизни. Без сомнения, еще слишком рано ставить точку в изучении знаменитой египетской фигуры. Наука никогда не спешит с выводами, стремясь доказать свои предположения. А нам же остается лишь ждать и удивляться знаниям

Полезно вспомнить

Треугольник

Треугольник прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Треугольника (в геометрии)), имеющими попарно по одному общему концу (вершины Треугольника (в геометрии)). Треугольник, у которого длины всех сторон равны, называется равносторонним, или правильным, Треугольник с двумя равными сторонами — равнобедренным. Треугольник называется остроугольным, если все углы его острые; прямоугольным  — если один из его углов прямой; тупоугольным — если один из его углов тупой. Более одного прямого или тупого угла Треугольник (в геометрии) иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Треугольник (в геометрии) равна ah/2, где а — любая из сторон Треугольника, принимаемая за его основание, a h — соответствующая высота. Стороны Треугольника подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон.

Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.

• Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
• Любой многоугольник можно разбить на треугольники — этот процесс называется триангуляция.
• Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Типы треугольников

По виду углов

Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

По числу равных сторон

• Разносторонним называется треугольник, у которого длины трёх сторон попарно различны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
• Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Правильный

Тупоугольный’

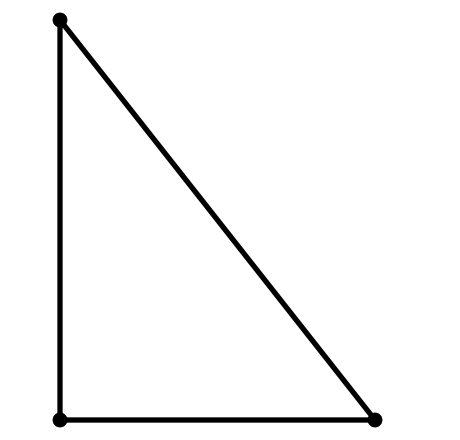
Прямоугольный

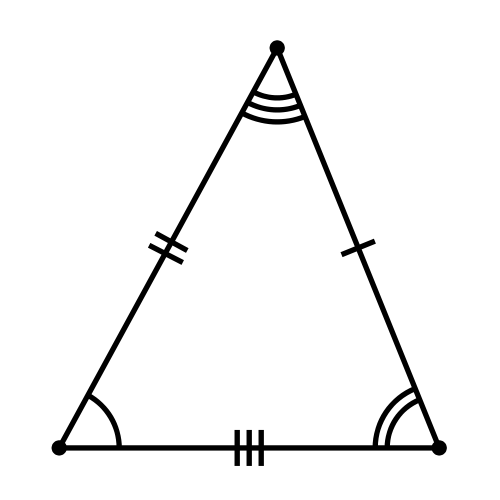
Разносторонний

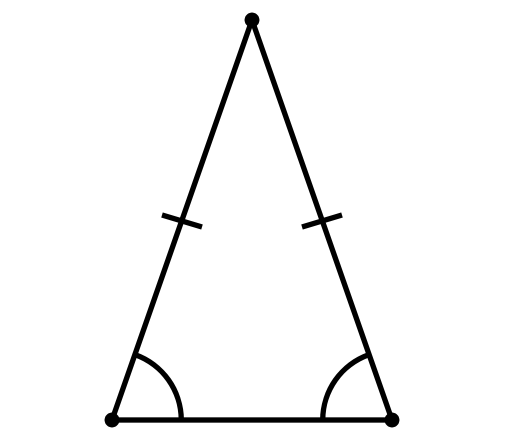
Равнобедренный

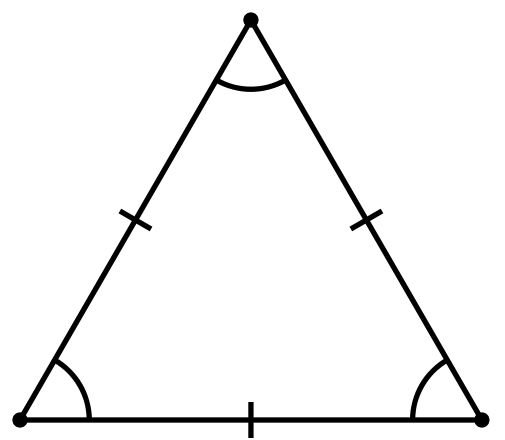
Равносторонний

Остроугольный

Окружности треугольника

Файл:Треугольник АВС и его окружности.png

Треугольник АВС и его окружности: вписанная (синяя), описанная (красная) и три вневписанных (зеленые)

Окружности, проходящие через вершины треугольника

• Описанная окружность (см. рис. справа) — окружность, проходящая через все три вершины треугольника. Описанная окружность всегда единственна, если треугольник не вырожден особым образом, т. е. две из трех его вершин не совпадают.
• Окружность Джонсона — окружность, проходящая через две вершины треугольника и через его ортоцентр. Радиусы всех трех окружностей Джонсона равны. Окружности Джонсона являются описанными окружностями треугольников Гамильтона, имеющих в качестве двух вершин две вершины данного остроугольного треугольника, а в качестве третьей вершины имеющих его ортоцентр.

Окружности, касающиеся сторон треугольника или их продолжений

Вписанная окружность (см. рис. справа) — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром
Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна. Точка Жергонна изотомически сопряжена точке Нагеля (см. ниже).

.

Вневписанная окружность(см. рис. справа) — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр — центр вписанной окружности срединного треугольника, называемый центром Шпикера или точкой Шпикера
Отрезки, соединяющие вершины с точками касания вневписанных окружностей с вершинами, пересекаются в одной точке, называемой точкой Нагеля.
.

Файл:Окружности Мальфатти.png

Окружности Мальфатти

Три окружности Мальфатти треугольника (см. рис. справа). Каждая из них касается двух сторон треугольника и двух других окружностей Мальфатти
Если провести три прямые, соединяющие центр каждой окружности Мальфатти с точкой касания между собой двух других, то они пересекутся в одной точке в точке Аджима-Мальфатти(=Ajima-Malfatti Point= http://faculty.evansville.edu/ck6/tcenters/recent/ajmalf.html).
.

Файл:Полувписанные окружности.png

Полувписанные окружности

• Три полувписанные окружности или окружности Веррьера (см. рис. слева). Каждая из них касается двух сторон треугольника и описанной окружности внутренним образом

  Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную.

• Лемма Веррьера. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности (инцентр).

Замечание

Вообще говоря, окружностей типа окружностей Веррьера, касающихся двух сторон треугольника и его описанной окружности, существует не три, а шесть: три внутренних и три внешних. Три последние касаются продолжений двух сторон треугольника и внешним образом описанной окружности. Для них можно ввести свою точку Веррьера.

Окружности, взаимно касающиеся друг друга внутри треугольника

• Три окружности Мальфатти попарно касаются друг друга внутри треугольника. (см. выше)
• Окружность девяти точек или окружность Эйлера касается вписанной окружности внутри треугольника в точке Фейербаха.

Окружности, взаимно касающиеся друг друга вне треугольника

• Три окружности Веррьера касаются описанной окружности вне треугольника.
• Окружность девяти точек или окружность Эйлера касается трех вневписанных окружностей вне треугольника внешним образом (Теорема Фейербаха, см. рисунок).

Файл:Circ9pnt3.svg

Иллюстрация к теореме Фейербаха. Точкой Фейербаха F считается наиболее близкая к вершине A отмеченная жирно точка на окружности

Окружность Аполлония касается трех вневписанных окружностей вне треугольника внутренним образом (см. рисунок)

Файл:Apollonius point.svg

Другие окружности

Файл:Окружность Ламуна.png

Окружность Ламуна

Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.

Файл:Окружность Конвея.png

Окружность Конвея

Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, отрезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея.

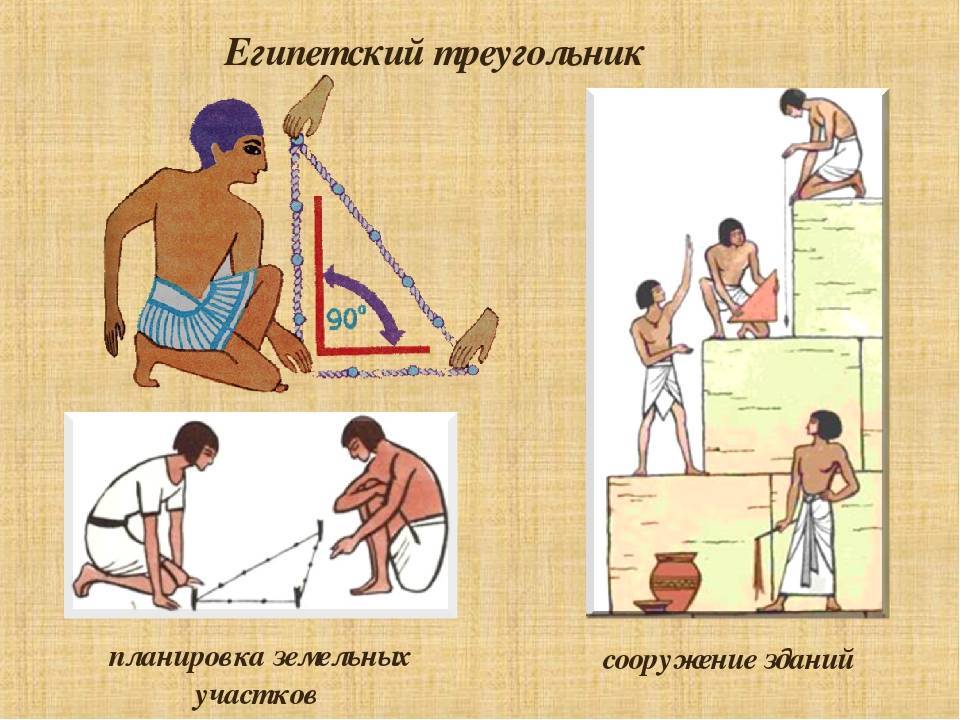
Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.